[새책] ‘메타생각’, “수학은 상상력의 학문” 생각의 점화장치를 격발시켜라

Life & Car

[새책] ‘메타생각’, “수학은 상상력의 학문” 생각의 점화장치를 격발시켜라

OSEN 강희수 기자

발행 2014.02.20 07: 55

최근 온라인에서 ‘구구단 필요 없는 곱셈법’이 화제가 된 적이 있다. 초등학생 시절, 배움의 길이 만만치 않다는 것을 보여주며 첫 번째 좌절감을 안겼던 구구단. 그 구구단이 없이도 곱셈 값을 구한다는 건 네티즌의 격한 관심을 끌기에 충분했다. 그저 작대기만 몇 개 그었을 뿐인데 답이 떡하니 나오니 말이다.

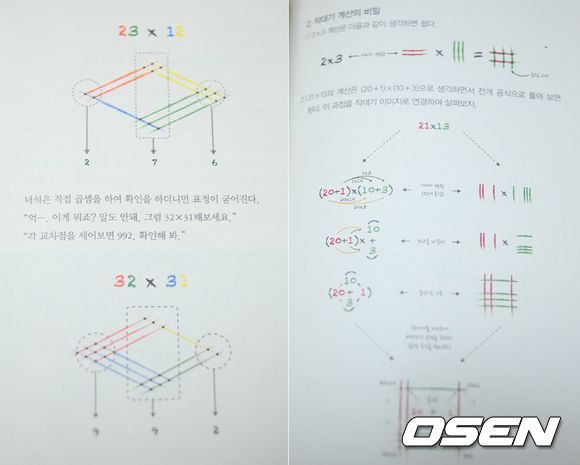
온라인에서 이슈가 된 두 자릿수 곱셈법은 10자리, 1자리 수만큼 서로 교차되게 선을 긋고 선과 선이 만나는 점의 숫자를 더해 곱셈 값을 구하고 있다. 네티즌들은 선 긋기만으로 곱셈값을 구할 수 있다는 사실에 크게 환호했다.

그런데 ‘구구단 필요 없는 곱셈법’은 단순히 ‘신기한 현상’ 일 뿐일까? 정확한 곱셈값이 나오는 이유를 수학적으로 증명할 수는 없을까?

이처럼 우리 주변에서 ‘신기한’ 범주에 속하는 것들을 모아 먼저 호기심을 유발하고 그 원리에 조심스럽게 접근해 나가는 방법을 구사한 책이 나왔다. 리콘미디어에서 출간한 ‘메타생각(META-THINKING, 부제:생각의 2중 스캐닝)’이 그것이다.

저자 임영익 씨는 스스로도 독특한 인생 이력을 지녔다. 서울대에서 생명과학을 전공하고 미국에서 뇌과학과 심리학을 공부했지만 귀국해서는 사법시험에 합격해 변호사가 됐다.

자신을 “공부하고는 인연이 없었던 학생”으로 표현하고 있는 저자는 고등학교 1학년 겨울방학 때 신기한 경험을 하면서 수학에 흥미를 갖기 시작했다고 말한다. 그림을 그려가면서 수학을 풀어보니 이해가 쉽더라는 것이다. 어려운 말로 ‘이미지를 이용하는 직관적 사고법’이라고 저자는 정의 내린다.

저자가 수학에 관심을 갖게 된 계기가 그랬던 것처럼, ‘메타생각’에 소개 된 에피소드들은 신기하고 재미있다. ‘구구단 없는 곱셈법’도 그 중의 하나다. 책 초반부에서 흥밋거리로 읽히기 시작한 에피소드들은 그러나 자신도 모르는 사이에 정교한 수학적 원리에 접근해 간다. 결국 저자가 이 책에서 독자들에게 주고자 하는 것은 ‘생각을 격발시키는 생각의 점화장치’다. 이 책이 독자들의 생각을 격발시키는 점화장치가 됐으면 하는 바람이 들어 있다.

책 서두에 나오는 추천사에도 독자의 의도가 잘 드러나 있다. 미국 Argonne 국립연구소 선임연구원인 노희석 박사는 “이 책을 보는 순간 머리에 ‘땅’하는 충격이 왔다”라고 적고 있다. 창의적 발상의 과정 속에 ‘메타생각’이라는 새로운 생각이 숨어 있다는 것이다. 저자가 책을 펴낸 의도가 제대로 먹힌 셈이다.

정운찬 전 국무총리는 추천사에서 “이 책은 창의적 사고가 무엇인지를 소개하는데 그치지 않고 어떻게(how) 할 수 있는가에 대한 실질적인 방법론을 제시한다”라고 적었다.

저자가 이 책을 통해 궁극적으로 도달하고자 하는 지점은 분명히 ‘잘 생각하는 법’이다. 그러나 그 방법이 어렵고 복잡하다면 자기 모순이다. 저자는 이 모순을 고교시절 수학책에서 경험했다.

원래 수학이라는 게 ‘생각하는 법’이 많이 숨어 있는 재미있는 책인데, 정작 학창시절 교과서로 쓰는 수학책에는 알 수 없는 개념과 낯선 기호들로 가득 차 있다. 마치 외계인의 언어처럼 보이는 수학에 익숙해지기 위해 무작정 외우기를 반복한다. 그 순간 ‘생각하는 법’은 점점 뒷전으로 밀리고 만다. 그 해결책으로 저자가 찾은 방법이 바로 ‘이미지로 생각하는 기술’이다.

저자는 수학에 흥미를 잃어버린 중3 학생을 붙들고 다시 수학에 재미를 붙이도록 유도하는 과정을 대화형으로 적었다. 마치 한 권의 소설책을 보는 듯해 읽어 가는데 막힘이 있다. 처음에는 수학이 신기하고 재미있게 느껴지도록 가벼운 에피소드에서부터 시작해 조금씩 빠져들게 하고 점점 수학적 원리에 가까이 가고 있다.

이 과정에서 작대기 긋기로 곱셈을 하는 셈법이 등장하고 삼각형의 내각의 합이 180도라는 것을 보여주기 위해 다리 찢기를 하고 있는 체조선수 사진도 등장한다.